1. 가설검정
: 모집단에 대해 어떤 가설을 설정하고 그 모집단으로 부터 추출된 표본을 분석함으로써 그 가설이 틀리는지 맞는지 타당성 여부를 결정(검정)하는 통계적 기법
- 검정통계량(Test Statistic): 연구자에 의해 설정된 가설은 표본을 건거로 하여 채택여부를 결정짓게 되는데 이때 사용되는 표본통계량
- 가설 검정(Hypothesis Testing): 검정통계량의 표본분포에 따라 채택 여부를 결정짓는 일련의 통계적 분석과정
1) 가설 검정의 절차
① 가설의 설정
집단의 특성을 파악하기 위해서 표본을 이용한 의사결정은 오류의 가능성이 상존한다. 따라서 가설 검정은 오류의 가능성을 사전에 관리하는 것이 중요하다. 오류의 허용확률을 정해놓고 그 기준에 따라 가설의 채택이나 기각을 결정한다.
- 귀무가설(Null Hypothesis, H₀): 현재 통념적으로 믿어지고 있는 모수에 대한 주장 또는 원래의 기준이 되는 가설
- 대립가설(Alternateive Hypothesis, H₁): 연구자가 모수에 대해 새로운 통계적 입증을 이루어 내고자 하는 가설
② 유의수준 α
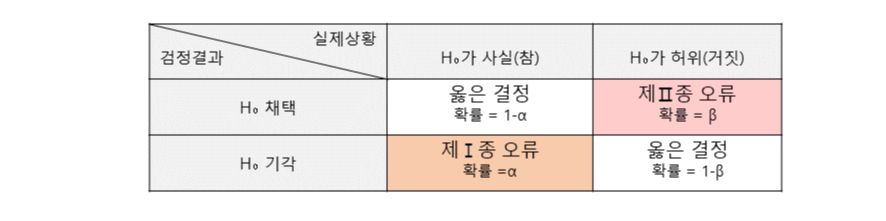
- 제 1종 오류: 귀무가설이 참일 때 귀무가설을 기각하도록 결정하는 오류
- 제 2종 오류: 귀무가설이 거짓인데 귀무가설을 채택할 오류, 또는 대립가설이 참일 때 귀무가설을 채택하도록 결정하는 오류
- 유의수준 α : 제 1종 오류를 범할 확률의 최대 허용 한계, 즉 표본에서 얻은 표본통계량이 기각역에 들어갈 확률
- p-value(유의확률): 관찰된 데이터 검정통계량이 귀무가설을 지지하는 정도를 확률로 표현한 것
- p-value가 작을수록, 유의수준 α 가 클수록 연구자는 귀무가설을 기각하고 자신의 주장에 확신을 가질 수 있음
- α값이 0.05라는 것은 95% 신뢰수준을 의미
2) 검정통계량 및 표본분포의 결정
3) 기각역의 결정
표본에서 계산된 통계량이 가설로 설정한 모집단의 성격과 현저한 차이가 있을 경우에는 모집단에 대해 설정한 귀무가설을 기각하게 된다.
- 기각역: 귀무가설을 기각하게 되는 검정통계량의 범위
- 임계치: 기각역의 경계값, 주어진 유의수준 α에서 귀무가설의 채택과 기각에 관련된 의사결정을 할 때 그 기준이 되는 점
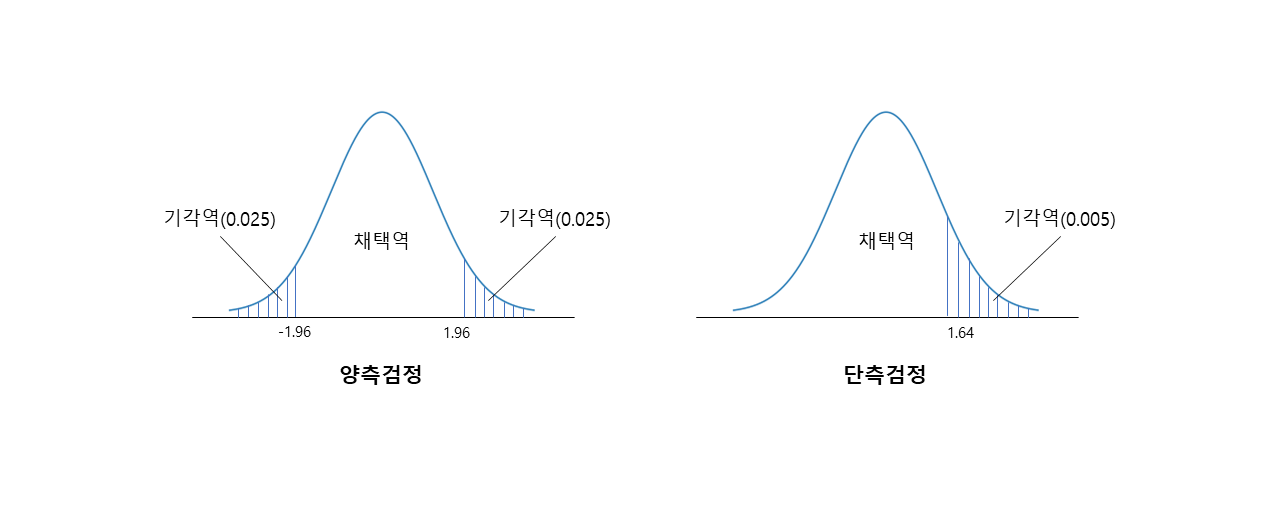
- 양측 검정: 가설 검정에서 기각영역이 양쪽에 있는 것
- 단측 검정: 가설 검정에서 기각영역이 어느 한쪽에만 있는 것
4) 검정통계량의 계산
① 의사결정
표본의 관측치로부터 계산된 검정통계량의 값이 기각역에 속하면 귀무가설을 기각하며(대립가설을 채택), 그렇지않으면 귀무가설을 채택(대립가설을 기각)한다.
② 통계량의 계산과 임계치의 비교
임계치가 결정되면 표본에서 얻은 통계량이 기각영역에 속하는지 채택영역에 속하는지를 결정해야 한다.
③ p-value
주어진 자료로서 귀무가설을 기각하려고 할 때 필요한 최소의 유의수준을 의미
- p-value < α : 귀무가설을 기각
- p-value > α : 귀무가설을 채택
'자격증 > 빅데이터분석기사' 카테고리의 다른 글
| [빅데이터분석기사 실기] train, test 데이터의 범주가 서로 다른 경우 (0) | 2024.06.15 |
|---|---|
| [빅데이터분석기사 실기] 총 정리 - 깃허브 (0) | 2024.05.28 |
| [빅데이터분석기사 실기] 제3유형: 통계적 가설검정(2) (0) | 2024.05.28 |
| [빅데이터분석기사 실기] 제2유형: 데이터 분석 (0) | 2024.05.22 |
| [빅데이터분석기사 실기] 제1유형: 데이터 전처리 (0) | 2024.05.18 |
1. 가설검정
: 모집단에 대해 어떤 가설을 설정하고 그 모집단으로 부터 추출된 표본을 분석함으로써 그 가설이 틀리는지 맞는지 타당성 여부를 결정(검정)하는 통계적 기법
- 검정통계량(Test Statistic): 연구자에 의해 설정된 가설은 표본을 건거로 하여 채택여부를 결정짓게 되는데 이때 사용되는 표본통계량
- 가설 검정(Hypothesis Testing): 검정통계량의 표본분포에 따라 채택 여부를 결정짓는 일련의 통계적 분석과정
1) 가설 검정의 절차
① 가설의 설정
집단의 특성을 파악하기 위해서 표본을 이용한 의사결정은 오류의 가능성이 상존한다. 따라서 가설 검정은 오류의 가능성을 사전에 관리하는 것이 중요하다. 오류의 허용확률을 정해놓고 그 기준에 따라 가설의 채택이나 기각을 결정한다.
- 귀무가설(Null Hypothesis, H₀): 현재 통념적으로 믿어지고 있는 모수에 대한 주장 또는 원래의 기준이 되는 가설
- 대립가설(Alternateive Hypothesis, H₁): 연구자가 모수에 대해 새로운 통계적 입증을 이루어 내고자 하는 가설
② 유의수준 α

- 제 1종 오류: 귀무가설이 참일 때 귀무가설을 기각하도록 결정하는 오류
- 제 2종 오류: 귀무가설이 거짓인데 귀무가설을 채택할 오류, 또는 대립가설이 참일 때 귀무가설을 채택하도록 결정하는 오류
- 유의수준 α : 제 1종 오류를 범할 확률의 최대 허용 한계, 즉 표본에서 얻은 표본통계량이 기각역에 들어갈 확률
- p-value(유의확률): 관찰된 데이터 검정통계량이 귀무가설을 지지하는 정도를 확률로 표현한 것
- p-value가 작을수록, 유의수준 α 가 클수록 연구자는 귀무가설을 기각하고 자신의 주장에 확신을 가질 수 있음
- α값이 0.05라는 것은 95% 신뢰수준을 의미
2) 검정통계량 및 표본분포의 결정
3) 기각역의 결정
표본에서 계산된 통계량이 가설로 설정한 모집단의 성격과 현저한 차이가 있을 경우에는 모집단에 대해 설정한 귀무가설을 기각하게 된다.
- 기각역: 귀무가설을 기각하게 되는 검정통계량의 범위
- 임계치: 기각역의 경계값, 주어진 유의수준 α에서 귀무가설의 채택과 기각에 관련된 의사결정을 할 때 그 기준이 되는 점

- 양측 검정: 가설 검정에서 기각영역이 양쪽에 있는 것
- 단측 검정: 가설 검정에서 기각영역이 어느 한쪽에만 있는 것
4) 검정통계량의 계산
① 의사결정
표본의 관측치로부터 계산된 검정통계량의 값이 기각역에 속하면 귀무가설을 기각하며(대립가설을 채택), 그렇지않으면 귀무가설을 채택(대립가설을 기각)한다.
② 통계량의 계산과 임계치의 비교
임계치가 결정되면 표본에서 얻은 통계량이 기각영역에 속하는지 채택영역에 속하는지를 결정해야 한다.
③ p-value
주어진 자료로서 귀무가설을 기각하려고 할 때 필요한 최소의 유의수준을 의미
- p-value < α : 귀무가설을 기각
- p-value > α : 귀무가설을 채택
'자격증 > 빅데이터분석기사' 카테고리의 다른 글
| [빅데이터분석기사 실기] train, test 데이터의 범주가 서로 다른 경우 (0) | 2024.06.15 |
|---|---|
| [빅데이터분석기사 실기] 총 정리 - 깃허브 (0) | 2024.05.28 |
| [빅데이터분석기사 실기] 제3유형: 통계적 가설검정(2) (0) | 2024.05.28 |
| [빅데이터분석기사 실기] 제2유형: 데이터 분석 (0) | 2024.05.22 |
| [빅데이터분석기사 실기] 제1유형: 데이터 전처리 (0) | 2024.05.18 |
